Son aquellas fracciones que representan una misma cantidad, aunque el numerador y el denominador sean diferentes.
Por ejemplo, tenemos dos tortas iguales. De una torta nos comemos medio trozo y de la otra, nos comemos 2 cuartos de torta, ¿en cuál de las dos queda más cantidad de torta?
Amplificación de fracciones
Amplificar una fracción consiste en encontrar una fracción equivalente, pero con sus términos (numerador y denominador) mayores.
Para amplificar una fracción basta con multiplicar el numerador y el denominador por el mismo número
Simplificar una fracción
Simplificar una fracción consiste en encontrar una fracción equivalente, pero con sus términos (numerador y denominador) más pequeños.
Para simplificar una fracción debe existir un número entre el que podamos dividir el numerador y el denominador de manera exacta.
GUIA N° 6
TEMA: NÚMEROS FRACCIONARIOS
SUBTEMA: adición y sustracción de fracciones homogéneas
Para sumar o restar fracciones homogéneas, basta con operar los numeradores y conservar el mismo denominador.
Ejemplo:
En el ejercicio anterior podemos apreciar que se efectúo únicamente la suma entre los numeradores de las fracciones, y el resultado conserva el denominador de 4.
Resolviendolo gráficamente tendríamos
Analicemos otro ejemplo, pero ahora restando
En este ejercicio se efectúa la resta únicamente entre los numeradores y el resultado conserva el mismo denominador de 5.
GUIA N° 7
TEMA: NÚMEROS FRACCIONARIOS
SUBTEMA: adición y sustracción de fracciones heterogéneas
Si representamos las unidades con círculos entonces las expresiones y se pueden representar así:

Lo primero que debemos hacer para sumar fracciones con distinto denominador, es encontrar un denominador común. Para ello, debemos encontrar el mínimo común múltiplo de los denominadores de las fracciones que sumamos. Veámoslo en un ejemplo.
Supongamos que queremos sumar:

Como las fracciones tienen diferente denominador, necesitamos ponerlas todas en uno mismo. Para ello, hacemos el mínimo común denominador, es decir, el mínimo común múltiplo de los dos denominadores.
Primero factorizamos los dos denominadores: 4 y 3 en factores primos.

VIDEO EXPLICATIVO
GUIA N° 9
TEMA: GEOMETRÍA
SUBTEMA: CUADRILÁTEROS Y SU CLASIFICACIÓN
1- ¿Qué son los cuadriláteros?
Los cuadriláteros son polígonos de cuatro lados y la suma de sus ángulos interiores es igual a 360°.
2- Clasificación de cuadriláteros
Los cuadriláteros tienen tres clasificaciones principales: paralelogramos, trapecios y trapezoides.
2.1- Paralelogramos
Son los cuadriláteros que tienen los lados paralelos dos a dos.
Se clasifican en:
2.2- Trapecios
Cuadriláteros que tienen dos lados paralelos, llamados base mayor y base menor. Se clasifican en:
2.3- Trapezoides
Cuadriláteros que no tiene ningún lado igual ni paralelo.
GUIA N° 10
TEMA: GEOMETRÍA
SUBTEMA: TRASLACIÓN Y SEMEJANZA
GUIA N° 4
Relaciones de orden entre números decimales
Para comparar números decimales puedes comparar las partes enteras de los números decimales entre sí y luego las cifras decimales según su posición, comenzando por la de mayor valor ( décimos), hasta que una de ellas sea de menor o mayor que la otra.
Por ejemplo, comparar 4,25 y 4,21
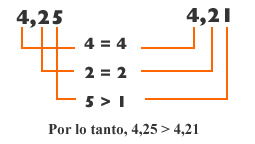
Otro caso es cuando tenemos números decimales, con distintas cantidades de cifras decimales después de la coma.
Para comparar si un número decimal es mayor, menor o igual a otro podemos igualar con ceros las cifra decimales para que cada cantidad tenga el mismo número de cifras decimales después de la coma.
Ya igualadas las cifras procedemos a comparar y a ubicar en la posición que le corresponde.
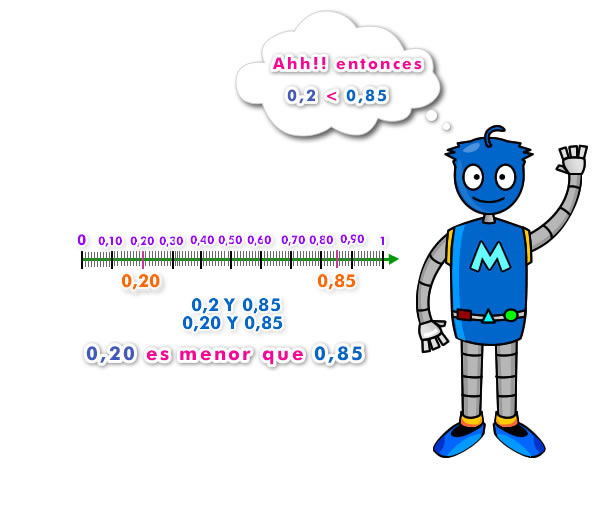
En el siguiente ejemplo queremos saber Cuál número es mayor entre 0,2 y 0,85. Observa en la gráfica que lo primero que se hace es igualar el número de cifras decimales agregando ceros a la derecha, para luego poder compararlas.
GUIA N° 3

Décimas y centésimas
Las unidades decimales se obtienen al dividir 1 unidad en 10 partes iguales, en 100 partes iguales. Si dividimos la unidad en 10 partes iguales, cada parte es una décima.
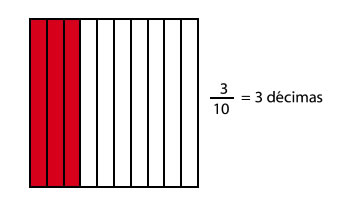
Si dividimos la unidad en 100 partes iguales, cada parte es una centésima. 1 unidad = 100 centésimas.
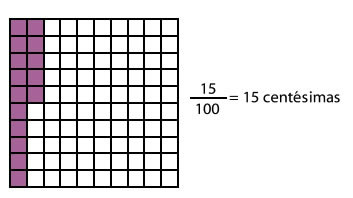
GUIA N° 2
Una fracción decimal es aquella en la cual el numero de abajo, o sea el denominador, es una potencia de diez, como sería 10; 100; 1000; 10000, etc. Es posible entonces escribir fracciones que sean decimales con un punto decimal y sin el denominador. Esto facilita enormemente el calcular las operaciones, tales como las sumas o multiplicaciones de la fracciones. Los números decimales son en si un tipo de número fraccionario. Por ejemplo el decimal 0.5 representa exactamente la fracción 5/10. La fracción 43/100 es también la representación de un decimal, es lo mismo entonces que 0.43. Veamos algunos otros ejemplos más claros:
Las fracciones decimales son entonces lo que corresponde a las partes de un entero que se ha partido en una decena de partes iguales o una centena, etc., etc. Es muy importante tener en claro que lo que generalmente llamamos números decimales, o sea los números con coma decimal, están expresando una fracción decimal.
GUIA N° 1
¿Qué son los números decimales?
Los números decimales se utilizan para representar números más pequeños que la unidad.
Los números decimales se escriben a la derecha de las Unidades separados por una coma. Es decir:
Centenas Decenas Unidades , Décimas Centésimas Milésimas
En la imagen que aparece a continuación, el primer cuadrado representa la Unidad. Si esta unidad la dividimos en 10 partes iguales (segundo cuadrado), representaremos las Décimas. Si las décimas las dividimos en 10 partes iguales o la unidad en 100 partes iguales (tercer cuadrado), representaremos las Centésimas.

Ejemplos de números decimales
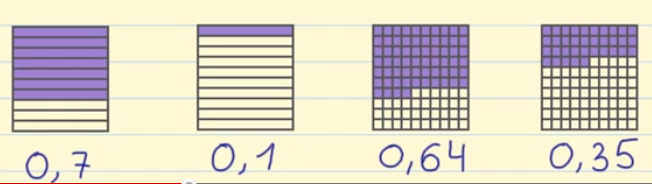
- Primer ejemplo: Si la unidad la dividimos en 10 partes iguales, tendremos décimas. Y hemos coloreado 7 de estas partes. La forma de escribirlo es 0 unidades, 7 décimas = 0,7
- Segundo ejemplo: En el segundo ejemplo también tenemos décimas y tenemos coloreadas 1. Se escribirá de la siguiente forma: 0 unidades, 1 décima = 0,1
- Tercer ejemplo: En el tercer ejemplo tenemos representadas centésimas, de las cuales tenemos coloreadas 6 décimas y 4 centésimas. Por lo tanto se escribirá: 0 unidades, 6 décimas 4 centésimas = 0,64
- Cuarto ejemplo: Tenemos centésimas (la unidad entre 100), de las cuales tenemos coloreadas 3 décimas y 5 centésimas. Lo escribiremos: 0 unidades, 3 décimas 5 centésimas = 0,35
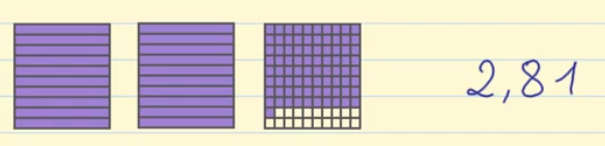
- Quinto ejemplo: Tenemos dos unidades enteras coloreadas y de la tercera unidad, que está dividida en centésimas, tenemos 8 décimas coloreadas y una centésima coloreada. Por lo tanto, se escribirá: 2 unidades, 8 décimas 1 centésimas = 2,81
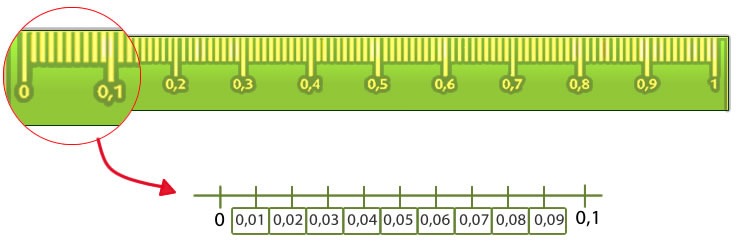
Números decimales en la recta numérica
Para ubicar números decimales en la recta numérica debes seguir los siguiente pasos:
1- Ubicar los números en orden, de menor a mayor, manteniendo la misma distancia entre dos números consecutivos.
2- Para ubicar los décimos se divide la distancia entre dos números consecutivos en 10 partes iguales.
3- Para ubicar los centésimos se divide la distancia entre dos números consecutivos en 100 partes iguales.
Por ejemplo:

En este caso en la recta numérica se ha dividido la unidad en 100 partes iguales y se han ubicado los centésimos. Entre el 0 y el 0,1 se ubican: